Algebraic simplifying radical expressions is converting an expression with a radical into a simpler form and, if feasible, removing the radical. Now let’s review the definition of radical expressions. Algebraic expressions incorporating radicals are known as radical expressions. The roots of algebraic expressions make up radical expressions.
Radical expressions can be simplified by taking them down to their most basic form and, if feasible, eliminating all of the radicals. The root might be an nth root, a square root, or a cube root. With the aid of solved examples, we will study the procedures for simplifying radical equations with variables—also, exponents and the principles for doing so.
What is Simplifying Radical Expressions?
Changing a radical statement into a simpler or alternative form is known as simplifying radicals. In general, it is applying the method of simplifying expressions to radicals.
Radical expressions are simplified by taking them to their most basic form and eliminating the radical. When a radical expression appears in the denominator of an algebraic expression. The radical expression is simplified by multiplying the numerator and denominator by the corresponding radical expression.
How to Simplify Radicals?
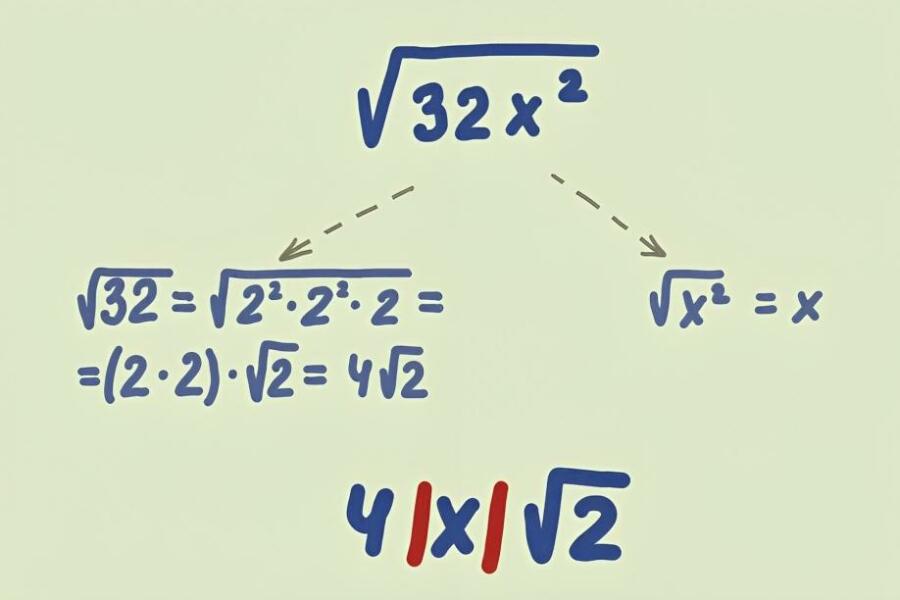
● While assessing radicals, there are four procedures to bear in mind. It resembles the process of estimating square roots while using a calculator.
● Determine the prime factorization of the integer under the radical sign. As the initial prime number, you’ll often start with 2, and then you may use numbers like 3 and 5. Continue until only prime numbers remain from the initial number.
● Find out what the radical’s index is. Remember that if you see the square root symbol, this is an index of 2. Before the radical sign, a small number should identify the index for any other indices.
● This value will inform you of the necessary repetitions of prime numbers following factorization to transfer the given value from within to outside the radical. To shift a prime number outside a cube root, you would need to find it three times using prime factorization.
● Simplify to clean up what you’ve got. Multiply the numbers you have moved outside together if you have moved more than one group of numbers outdoors. The remaining prime numbers inside the radical should be treated similarly. When evaluating radicals, the final step is to simplify expressions. You’ll then learn the outcome.
Radicals with Various Integers inside The Root Should Multiply
If you know the proper method, multiplying radicals with different integers inside the root is not a tough process. Understanding the square root multiplication feature is essential to using this technique. Once you have it, you may use the product rule to simplify complex expressions. The Product Raised to a Power Regulation is another name for this regulation. Any equation with a radical may be made simpler using the Product Rule. The denominator is multiplied by the same nonzero factor as the numerator.
To do this, all the terms must be combined just like with a polynomial. For instance, you would need to multiply the denominator by 3 to multiply it by 5 instead. By doing this, the radical will be taken out of the equation. The output will be the same as the original radical since the Product Rule for Radicals uses a commutative technique. The key implication of this technique is that radicals may also be simplified using it.
Radicals are frequently simplified more easily than they appear. This is because you may multiply all the terms in an equation to make it simpler using the distributive property. You are not able to multiply the radicals directly using this technique. It is crucial to remember that the words can only be combined if their indices match. In other words, the radicand’s index and square root must be the same.
Split Radicals with Various Roots and Integers

Dividing radicals with various roots by different integers is trickier than other operations. To complete this stage of the equation, it is necessary to comprehend a few important ideas. Using a table of multiples may also be beneficial. Using these resources, you can simplify your issue and find the necessary solution.
Using a method called the quotient rule, radicals having distinct integers inside the root may be divided. In this case, a radical is employed instead of a fraction to divide integers. You must ensure that the degrees of the two radicals are comparable and that their indices are the same.
The square root method is another approach to split radicals with various integers inside the root. The root, in this instance, is the word with the greatest number. Adding the two roots together is one number that may be divided and multiplied to create a new radical. To make this work, you must be familiar with the proper formula.
Having A Radical in The Denominator Simplifies Radicals
Having the ability to simplify radicals with a radical in the denominator is tremendously beneficial. The radicals in the fraction’s denominator can be removed by employing this method. The radical values will be simpler to assess as a result. You might also find it useful for other radical operations, including multiplying and dividing.
It would help to use all the integer operation rules while simplifying radicals. The quotient rule is included in this. To simplify radicals, you may also employ prime factorization and rational exponents. The prime factorization algorithm looks for pairs of related factors. The product is then defined as these factor groupings. The quotient will be the product of each component, as each group consists of two factors. The exponent on the remaining factor will be the remainder.
When attempting to simplify a fraction, you have two options: utilise the quotient rule or the denominator’s binomial conjugate. Any of these techniques will decrease the number of radicals in the denominator. Removing any factors that are not perfect roots from the denominator is necessary. The square root of three is not a perfect root. Hence, you must multiply the numerator and denominator by 3 squares.
Also read: The Concept of How to Find The Domain of A Function
























































