The concept of velocity plays a significant role in subjects like Statics, Dynamic Mathematics, and kinematics. And for the various forms of motions that are affiliated with these particular systems, these systems support a different velocity formulas for the velocity of an object that is a part of that particular system.
To apply the correct formula for the solution of the velocity, many factors need to be considered—for example, the type of motion that the object supports, translation, or circular motion.
Following the instructions stated below, you will be able to apply the accurate formula to a problem and find the most appropriate solution to the problem.
Velocity Formulas when Acceleration is Constant
- This is the formula for velocity used for the time measure and the constant acceleration supported by an object, and either one of the initial or the final velocities of that particular object is known to us. Using this formula, we will be able to compute the other one.
- This is the velocity formula that helps us identify the measure for the displacement of an object. For this formula, the values of the object’s acceleration, the total time is taken, and the initial velocity are needed.
- If the final velocity is known to us instead of the initial velocity, we can use the formula (1) to find the value of the initial velocity.
- This is the formula for the velocity of an object that is used when the time factor does not restrict the object’s motion for that particular interval of the motion. Or, this formula is used when the value for the time taken is unknown to us.
Velocity Formulas Free of Acceleration
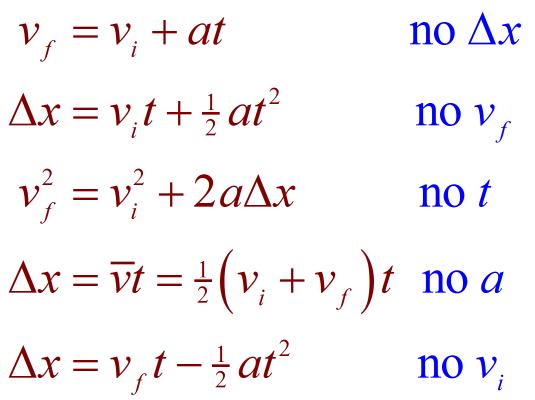
These formulas are associated with the very basic concepts of velocity, just like how velocity can be constant and variable. Following either of the two, a set of formulas can easily be derived from those conditions. And here are some of those:
- This formula stands true whether the velocity is constant or variable, as it deals with the entirety of the motion that the particular object is subjected to instead of only a small intersection of it. As per this formula, the average velocity of an object is the ratio of the total displacement covered by the given object to the total time taken.
This formula is applicable irrespective of the value of acceleration. For this, the acceleration can be zero, unity, or constant.
2. This is the velocity formula applicable when an object’s initial and final velocity is known to us. And to find the average of both those velocities, the mean of the two given velocities is used as the appropriate value.
3. This is the formula for the average velocity of an object that is only in correspondence with the displacement and the time it takes for the object to travel that displacement. As this formula does not comprise any velocity factor, it applies to objects undergoing uniform and variable velocity.
This formula is also used to give an object’s instantaneous velocity when it has a variable velocity.
4. This is the formula for an object’s instantaneous velocity when it has a uniform velocity.
Comparing formulas (4) and (3), formula (3) satisfies formula (4), for all the values of displacement and time interval.
All these formulas are independent of the value o the acceleration and therefore are relatively easier to use. But for most cases, these formulas are used only for the linear (or 1-dimensional) motion. But these can be used about the velocity with constant acceleration to a certain extent.
However, all the formulas given for the constant acceleration are applicable when the acceleration is not known (like the formulas mentioned above).
Velocity Formulas for Circular Motion

When an object is in a circular motion, the centripetal or centrifugal force is bound to act over it. But, in most cases, the velocity of the object is always constant for either of these two. And, therefore a new term is brought about in this concept, called angular velocity.
Angular velocity correlates with the measure of arc distance that the object traces in the unit of time taken.
Also, in a circular motion, the acceleration changes at every instant point that it is measured from, even though its magnitude continues to be the same.
- This is the measure of the linear velocity associated with the particular undergoing the circular motion. This is the constant value that will always be associated with the object as long as the object continues to be in motion.
This is the formula to compute the angular acceleration or the object’s linear velocity without accounting for the object’s angular velocity.
2. This is the formula that signifies the relation between the angular velocity of an object and the angular acceleration (or the centripetal or centrifugal acceleration) associated with that object.
3. This is one of the fundamental formulas associated with a circular motion and its affiliated fragments. The formula states the relation between the same body’s angular velocity and linear velocity when it is undergoing a circular motion.
The concept of circular motion or angular units greatly depends on the measure of the circular path’s radius followed by a body that undergoes the aid motion. It is because the measure of that radius determines the extent of the displacement or the length of the arc followed by the object in a particular interval.
Also read: Math Tips That Helps in Your Math IB Exam
























































